The University of California has published a study of pedestrian crashes in Oakland, California,
The Continuing Debate about Safety in Numbers—Data from Oakland, CA
Judy Geyer, Noah Raford and David Ragland, Traffic Safety Center;
Trinh Pham, Department of Statistics, UC Berkeley
UCB-ITS-TSC-2006-3
The full report is available online:
http://www.escholarship.org/uc/item/5498×882
John Forester, founder of the Effective Cycling program of cyclist education, and statistician, has demonstrated that the Safety in Numbers claim of Jacobsen (also cited in the Oakland paper) is faulty. Due to faulty math, a random set of numbers will generate the curve that apparently shows a decreasing crash rate with increasing numbers of users. This is not to say that the safety-in-numbers claim is false, but rather that Jacobsen has provided no evidence to support it. (Forester also questions Jacobsen’s explanation for safety in numbers as applied to bicyclists, but that’s a different issue.)
The Oakland report expresses the same complaint about Jacobsen’s math, and goes on to use better math to look for answers. Here’s a quote from page 5 (PDF numbering) of the Oakland report:
However, others are concerned that correlating collision rate (C/P) with pedestrian volume (P), (where C equals collisions and P equals pedestrian volume) will almost always yield a decreasing relationship due to the intrinsic relationship of the variable P and the fraction 1/P.
Tom Revay has generated a Microsoft Excel Workbook demonstrating how Jacobsen’s curve may be generated with random data. Press the F9 key on a PC to refresh the random data. (Press Command [Apple] and = at the same time on a Mac. I thank Dan Carrigan for this information)
The Oakland study came up with some interesting and intriguing results. Here are a few; please correct me if I am wrong:
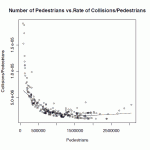
- The graph on p. 17, PDF numbering (click to see a larger version) shows the characteristic downward curve due to faulty math. However, the curve slopes back upwards for the intersections with the very highest numbers of pedestrians.
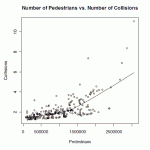
A better graph (graph on p. 16, PDF numbering, click to see a larger version) shows crashes increasing with a steeper slope for the higher-volume intersections, worst at the intersections with the highest volume. Crash numbers are low enough, though, that the results for individual intersections are not statistically significant.
- The Oakland study examines different intersections in the same community over the same time period rather than the same intersections at different times, or different communities with different volumes of pedestrian and vehicular traffic. The study can establish whether the safety in numbers effect applies only under the conditions it examined. Data from different times of day might possibly be checked against traffic volumes, though the results would be less robust and effects of lighting, alcohol use etc. would make them harder to interpret.
- It is clear that a few intersections are outliers, with many more crashes than others. These intersections would be high on a priority list for improvements — though the actual numbers for individual intersections, again, are too low to be statistically significant. The problem with lack of statistical significance highlights the importance of applying research data and operational analysis in determining where to make infrastructure improvements — crash data for an individual intersection are not statistically robust unless the intersection has an extremely bad problem. You apply research results and operational analysis so you can avoid collecting data on each intersection by killing and injuring people.
- (See Results, p. 9, PDF numbering) Number of lanes on the primary and secondary streets, and number of marked and unmarked crosswalks, did not correlate with crash rates! (But note that this result is consistent with data on bicycling showing that riding on arterials is safer than on residential streets).
- Despite the safety-in-numbers finding, the intersections with the largest numbers of crashes are still those with high pedestrian volumes. Increasing numbers decrease the rate of crashes, but not the number of crashes.
-
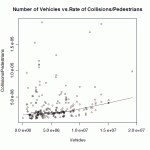
The crash rate increases for pedestrians as the number of vehicles increases (page 18, PDF numbering), though less rapidly than the number of vehicles. Is there a safety in numbers effect for vehicle operators as the number of vehicles increases? Yes, the likelihood that any particular driver will collide with a pedestrian decreases with the amount of vehicular traffic passing through an intersection — though the study doesn’t report this. The study doesn’t answer whether the result is achieved by improved signalization at high-volume intersections, or by depressing pedestrian volume (risk homeostasis), or by what other effect. The study also doesn’t say anything about crashes overall, as it doesn’t report on crashes not involving pedestrians.
All in all — interesting, intriguing, and careful research — but more research is needed!

Regarding Tom Revay’s Microsoft Excel Workbook. On Mac Excel version press the Command (Apple) and = keys to refresh the random data.
The misunderstanding of the math here amazes me. If C is an independent random variable — something with a mean value and then random variation about that mean — of course you’ll get an inverse curve if you plot C/P versus P. But the whole point is if risk to a pedestrian is NOT affected by the number of peds, then C should rise proportionally with P. If r = risk, then the number of crashes is expected to be E[C] = rP. If you generate crash figures by taking E[C] and then adding a random perturbation, then with enough data the perturbations wash out, and you end up plotting C/P = rP/P = r, which of course plots as a straight line. Restated, if risk is not affected by the number of peds, the shape of C/P versus P should be a horizontal line. The fact that it declines indicates that risk declines with number of pedestrians. This is not an artifact of using an inverse function.
What the spreadsheets that simply generate random values of C do, implicitly, is assume that the number of crashes is independent of the number of pedestrians. That assumption is tantamount to assuming the truth of safety in numbers, for if the number of crashes stays constant when the number of peds doubles or triples, the crash risk has definitely fallen with increased numbers of peds.
Furth’s first paragraph expresses the irrelevant obvious. Sure, if you calculate a constant risk then you get a horizontal line for C/P v P. However, if you don’t get a horizontal line from actual data, that shows little. After all, if you have data for C and matching data for P, just plot C against P and look at the curve. If the risk is constant, the curve will be a straight line from the origin at some slope, which is the risk.
Figure 3 from the Oakland pedestrian study does just that. That graph shows an approx straight line from just above the origin out to about 1.5Meg pedestrians. After that, it shows another approx straight line with a steeper slope from 1.5Meg to 3Meg. The steeper slope shows that the risk for a pedestrian goes up with the number of pedestrians. Don’t need any fancy math to see that.
Furth’s second paragraph incorrectly describes what was done regarding Jacobsen’s paper. I did it; I know what I did. I was not familiar with Brindley’s work of 1994, so I worked out my argument. Furth bases his comment on “spreadsheets that simply generate random values of C”. That’s not what I did. I worked with Jacobsen’s variables of Accidents (A), Number of Cyclists (C), and Population (P). He plotted A/C vs C/P and produced what gave the appearance of being descending hyperbolic curves. I generated independent random variables for each of A, C, and P. I also generated them to be within reasonable ranges of each other (for example, never more accidents than cyclists, never more cyclists than population). Whichever way I computed the random variables, the plot of A/C vs C/P over a hundred or so sets of random numbers produced curves that looked like Jacobsen’s curves. Therefore, I reported that the persuasive appearance of Jacobsen’s curves did not indicate a reduction in accident rate produced by increased numbers but was simply an artifact of the method of presentation.
The abstract of the Oakland report states that “the risk of collision for pedestrians decreases with increasing pedestrian flows, and it increases with increasing vehicle flows.” Yet as John Forester notes, the graph in Figure 3 of the report shows increasing risk with increasing pedestrian flows. Can anyone please help me understand this apparent contradiction?
I can describe part of the work in the study. There were masses of data of motor-vehicle volume on many streets, and, hence, of the volume of motor-vehicle traffic through many intersections. There were many fewer data items regarding pedestrian volumes at these intersections. Therefore, putative pedestrian volumes were calculated according to a program based on how pedestrians choose to travel. This produced calculated pedestrian volumes for the intersections for which motor-traffic volume data existed. The calculated pedestrian volumes were compared to some other measured pedestrian volumes, and the degree of agreement was considered to be satisfactory. Then both motor and ped volumes were plotted against reported car-ped collisions for each intersection. These data were plotted on two graphs, one of collision number against pedestrian number, the other of collision number against motor vehicle number.
The authors of the study state their aim: “The primary objective of this paper is to review the appropriate use of ratio variables in the study of pedestrian injury exposure. We provide a discussion that rejects the assumption that the relationship between a random variable (e.g., a population X) and a ratio (e.g., injury or disease per population Y/X)
is necessarily negative.”
In short, the authors are not really concerned with the actual relationship between volumes and collisions, but, instead, with the appropriateness of stating this in terms of ratios. In short, with my criticism of Jacobsen’s paper claiming that the car-bike collision rate decreases with increases in numbers of cyclists, I repeat, I did not disprove Jacobsen’s claim, but I did disprove that his method would demonstrate his claim.
In pursuit of their aim, the authors processed the ratios obtained from the obvious data of number of collisions vs. the number of pedestrians according to some kind of mathematical processing on which I am not sufficiently expert to produce an accurate criticism.
The authors state their null hypothesis: “the null hypothesis is that pedestrian injury risk is constant with respect to pedestrian volume.” That may be one null hypothesis, but it is not the appropriate null hypothesis, for nobody has been arguing that hypothesis.
The mathematical processing of ratios led the authors to conclude that the null hypothesis should be rejected. OK, that’s fine, collision rate does vary, in some way or other not recognized, according to number of pedestrians. The conclusion that the collision rate does vary with the number of pedestrians says nothing at all about which way it varies or with what shape. But the authors conclude that their mathematical processing of ratios demonstrates that: “the risk of collision for pedestrians decreases with increasing pedestrian flows.”
Well, look at the actual data as shown in Figure 3. That clearly shows that the slope of the line Collisions/Pedestrians, the collision rate, has a higher slope above about 1.5 Meg pedestrians than it has below about 1.5 Meg pedestrians.
The most reasonable conclusion is that the mathematical processing (which, I repeat I don’t understand well enough to produce a proper criticism) must be wrong, for it produces a result that is directly contrary to the actual data on which it is based. It is not a case of producing a prediction that does not agree with some other set of data, which could be for any number of reasons. It is the case of processing a given set of data that produces a mathematical statement that contradicts those original data.
It looks as though the concern about the criticism of Jacobsen’s use of ratios has overwhelmed consideration of the facts presented by the data.
I sent a link to this post to the authors of the study. None responded. I would hope they do, to address the question of disagreement of their conclusion of safety in numbers with the results shown in the graphs.
Their graphs and descriptions are not particularly helpful. Moving past figure 4, I am never sure whether we are using real data or the regression estimates. Moreover, I don’t know how much smoothing they are doing in figure 6. Consequently, I can’t say whether I agree with their “visual” assessment. It seems to be that one could explicitly fit this with a regression and report a coefficient so we could avoid squinting at the graph.
But only looking at Figure 3 obfuscates the marginal effect of more pedestrians due to the failure to control for neighborhood and vehicle effects. Think of Simpson’s Paradox. Similarly, the upswing in Figure 4 could be due to the correlation of pedestrian and vehicle counts.
I’m surprised that people are so accepting of the simulated pedestrian data. Even with a high coefficient of determination, one can have a crappy fitting model. Moreover, we can’t tell whether the fitted points — the 40 or so intersection with pedestrian counts — properly represent the population of intersections. A graph or two would be helpful in this question.
Anyway, I think that with the data and the regression results there one could tease out the answer to their question. But like JA and JF, either due to my failing or the paper’s, I can’t convince myself that we know the answer from the evidence presented.
I get the impression that this criticism of Jacobsen is confusing the interpretive graphics for the discussion section of the paper, with the actual analysis.
Jacobsen’s basic model is
Accidents = a Cycling^b
where a and b are parameters that need to be estimated. In a regression one would estimate this equation by taking the logarithm:
log(Accidents) = A + b log(Cycling)
Since he has cross-sectional data for cities with varying sizes and populations, we would expect that the value of A varies by city even if the sensitivity parameter b is meaningful across cities, so his actual regression model was
log (Accidents/Population) = A + b log (Cycling/Population)
He gets 95% confidence interval estimates for b that almost always are entirely below 1.0. His typical value is 0.4 but there is some variation.
So his final result would be
(Accidents/Population) = A (Cycling/Population)^0.4
So I am wondering how one would get that result with a bunch of random numbers. I doubt it. In fact, the criticism does not seem to even address the regression equations which lie at the heart of the study.
After reporting those results, they try to explain what it means. They multiply both sides by Population/Cycling to get
Accident/Cycling = A * (Cycling/Population)-0.6 which they proceed to graph. That’s so one can understand the relevance of their result for an individual cyclist, which is that the risk goes down even though–in that study–the total number of accidents goes down.
I certainly can imagine that bad data can give spurious results, but I just don’t see the Forester logic, or in general the complaint about their use of A/C against C/P given that this was just a final display after doing the analysis. Moreover, I am unclear how a random large measurement error in the data could cause their result, unless you were to hypothesize that the measurement error for accidents is negatively correlated with the measurement error for cycling. (An assumption which validates every statistical analysis ever done.)
Yes of course one might get the spurious result had the actual regression model been log(Accidents/Cycling) = A + b (Cycling/Population) but according to their paper, it wasn’t. So why all the energy attacking the model that they didn’t use?
Pingback: John S. Allen's Bicycle Blog » Safety in numbers: if and when so, why?
What John Forester did with random numbers is a distraction. I was the one who first performed function sensitivity analysis on the method used by Jacobsen, and I used a number of functions, including random data, and random noise in an Excel spreadsheet. I told John about this work and he replicated the result. Ezra Hauer has a nice paper on the Safety Performance Function, and what properties in must have in order to do analysis of the type Jacobsen attempted.
The main problems with Jacobsen’s analysis are not that there is a non-linear relationship between bicycle collisions and a reasonable exposure metric, since this has been known to be true for motoring traffic since Smeed first studied the issue, by curve fitting back in the late 1930s (though the relationship he found was not a correct general model – it only applied to the early days of motoring, not the present – which has been replaced by time series models that show an early Smeed like period, followed by an exponential decline in crashes versus time – See Koornstra work), or that random data (in general, any noise at the origin or any function that has a non-zero value at the origin will diverge), it is that he made two errors:
1) He used the epidemiological assumption of linear scaling of crashes with “exposure”, which if true would give the flat line Furth describes if the crash rate was a constant function of exposure; but that was never true for motoring, and is not true for cycling. This incorrect assumption sets an unrealistically high baseline, thus making his replication of Smeed’s curve look like something desirable. If he had instead compared bicycling crashes vs exposure to the present time series relationship used for motoring, he would have concluded that bicyclists are doing much worse than motorists as “exposure” increases.
2) His exposure metric was flawed. In general I am distrustful of survey data (2000 Census reported bike commuters) as opposed to measured data (he used SWITRS – measured CA State traffic data), and in particular, there is no evidence that all cycling: recreational, utility and commuting combined, scale linearly with commuting, and in particular, scale in a way that passes through the origin. I had the opportunity to use the same SWITRS bicycling crash data (but not the ped data) set and obtained Census data so I could do the exact same data analysis as Jacobsen. One thing I found was that Peter had purposely filtered the data to create the nice clean curves in his paper, by selecting for only those cities that a number of crashes for both bicycling and walking above an arbitrary per capita threshold rate, leading to his set of 68 cities. If one looks at the full data set for all 300+ cities, one finds a number of cities that had zero reported commuters and yet had bicycle crashes. This alone casts doubt on the assumption that reported commuting is a viable “proxy”, to use Jacobsen’s term, for all bicycling in a city, thus casting a cloud over his data analysis method.
In addition, he did one more thing which I find remarkably counterproductive. At best, his paper shows a correlation between lower reported commuting, and a higher crash counts. He speculated, without any data whatsoever, about a causal link for the correlation, by claiming that motorist compensation (seeing more cyclists made them less likely to collide with them) was the cause, and then reported this in his conclusions. A referee who understood that correlation is not the same as causality would have had him change his conclusions, and sadly many people have accepted this speculation as fact.
The influence of the Jacobsen paper is largely produced by the graphs, all of which claim to be evidence for Jacobsen’s thesis. All of these graphs are of the form A/B vs B/C, which on the basis of any data at all produce very persuasive quasi-hyperbolic curves.
Jacobsen claims that his thesis actually is I=aE^b, or Accident Number = a*(Cyclists Number)^b. The value for b on the basis of a least squared error estimate, averages about 0.4, as presented in a table.
But then Jacobsen displays graphs that display other functions, all of which fit the pattern A/B vs B/C. These are the graphs that most people believe demonstrate Jacobsen’s thesis. But they don’t; any such graphs look like these, regardless of the source of the data.
In short, Jacobsen is guilty of false advertising. If he wanted to show graphs, he should have shown them of his basic formulation, not of functions that arbitrarily form his desired function whatever the data.